History of mathematics VII

18th century

Leonhard Euler by Emanuel Handmann.

The most influential mathematician of the 1700s was arguably Leonhard Euler. His contributions range from founding the study of graph theory with the Seven Bridges of Königsberg problem to standardizing many modern mathematical terms and notations. For example, he named the square root of minus 1 with the symbol i, and he popularized the use of the Greek letter π to stand for the ratio of a circle's circumference to its diameter. He made numerous contributions to the study of topology, graph theory, calculus, combinatorics, and complex analysis, as evidenced by the multitude of theorems and notations named for him.

Other important European mathematicians of the 18th century included Joseph Louis Lagrange, who did pioneering work in number theory, algebra, differential calculus, and the calculus of variations, and Laplace who, in the age of Napoleon did important work on the foundations of celestial mechanics and on statistics.

[edit] 19th century

Behavior of lines with a common perpendicular in each of the three types of geometry

Throughout the 19th century mathematics became increasingly abstract. In the 19th century lived Carl Friedrich Gauss (1777–1855). Leaving aside his many contributions to science, in pure mathematics he did revolutionary work on functions of complex variables, in geometry, and on the convergence of series. He gave the first satisfactory proofs of the fundamental theorem of algebra and of the quadratic reciprocity law.

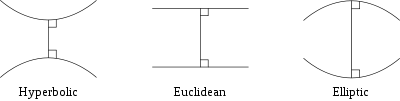
This century saw the development of the two forms of non-Euclidean geometry, where the parallel postulate of Euclidean geometry no longer holds. The Russian mathematician Nikolai Ivanovich Lobachevsky and his rival, the Hungarian mathematician Janos Bolyai, independently defined and studied hyperbolic geometry, where uniqueness of parallels no longer holds. In this geometry the sum of angles in a triangle add up to less than 180°. Elliptic geometry was developed later in the 19th century by the German mathematician Bernhard Riemann; here no parallel can be found and the angles in a triangle add up to more than 180°. Riemann also developed Riemannian geometry, which unifies and vastly generalizes the three types of geometry, and he defined the concept of a manifold, which generalize the ideas of curves and surfaces.

The 19th century saw the beginning of a great deal of abstract algebra. Hermann Grassmann in Germany gave a first version of vector spaces, William Rowan Hamilton in Ireland developed noncommutative algebra. The British mathematician George Boole devised an algebra that soon evolved into what is now called Boolean algebra, in which the only numbers were 0 and 1 and in which, famously, 1 + 1 = 1. Boolean algebra is the starting point of mathematical logic and has important applications in computer science.

Augustin-Louis Cauchy, Bernhard Riemann, and Karl Weierstrass reformulated the calculus in a more rigorous fashion.

Also, for the first time, the limits of mathematics were explored. Niels Henrik Abel, a Norwegian, and Évariste Galois, a Frenchman, proved that there is no general algebraic method for solving polynomial equations of degree greater than four. Other 19th century mathematicians utilized this in their proofs that straightedge and compass alone are not sufficient to trisect an arbitrary angle, to construct the side of a cube twice the volume of a given cube, nor to construct a square equal in area to a given circle. Mathematicians had vainly attempted to solve all of these problems since the time of the ancient Greeks.

Abel and Galois's investigations into the solutions of various polynomial equations laid the groundwork for further developments of group theory, and the associated fields of abstract algebra. In the 20th century physicists and other scientists have seen group theory as the ideal way to study symmetry.

In the later 19th century, Georg Cantor established the first foundations of set theory, which enabled the rigorous treatment of the notion of infinity and has become the common language of nearly all mathematics. Cantor's set theory, and the rise of mathematical logic in the hands of Peano, L. E. J. Brouwer, David Hilbert, Bertrand Russell, and A.N. Whitehead, initiated a long running debate on the foundations of mathematics.

The 19th century saw the founding of a number of national mathematical societies: the London Mathematical Society in 1865, the Société Mathématique de France in 1872, the Circolo Mathematico di Palermo in 1884, the Edinburgh Mathematical Society in 1883, and the American Mathematical Society in 1888.